Research Projects
Developing new engineering materials under extreme environments is crucial for today’s technological advancement and sustainable development, considering the conflict between energy use and climate change. As of 2020, 60% of the energy supply in the US still relies on thermal power plants from fossil fuels or wastes 1. Designing safer and cleaner power plants with less greenhouse gas emissions requires new engineering materials to sustain higher operational temperatures and repeated cyclic loading while maintaining mechanical stability and strength. Traditional refractory metals such as tungsten and its alloy suffer from brittleness and poor corrosion resistance at high temperatures, undermining their high-temperature ductility and overall strength. In recent decades, several classes of new engineering materials have become potential candidates for refractory materials, such as high-entropy alloys, metallic glasses, and metal-ceramic composites. Since defects and their interactions primarily control the mechanical properties of engineering materials, the underlying difficulties in designing these materials are the insufficient knowledge of their microstructures and defect evolutions.
My primary interest is investigating how microscopic defects in complex materials evolve under mechanical loading and extreme environments and thus accelerate the design of novel engineering materials. My research focuses on atom-scale modeling to develop predictive thermodynamic and kinetic theories of defect processes in response to mechanical deformation. I am also developing numerical analysis and advanced simulation methods to explore higher length- and time-scale models.
Predict the cross-slip rate of screw-dislocation in fcc nickel
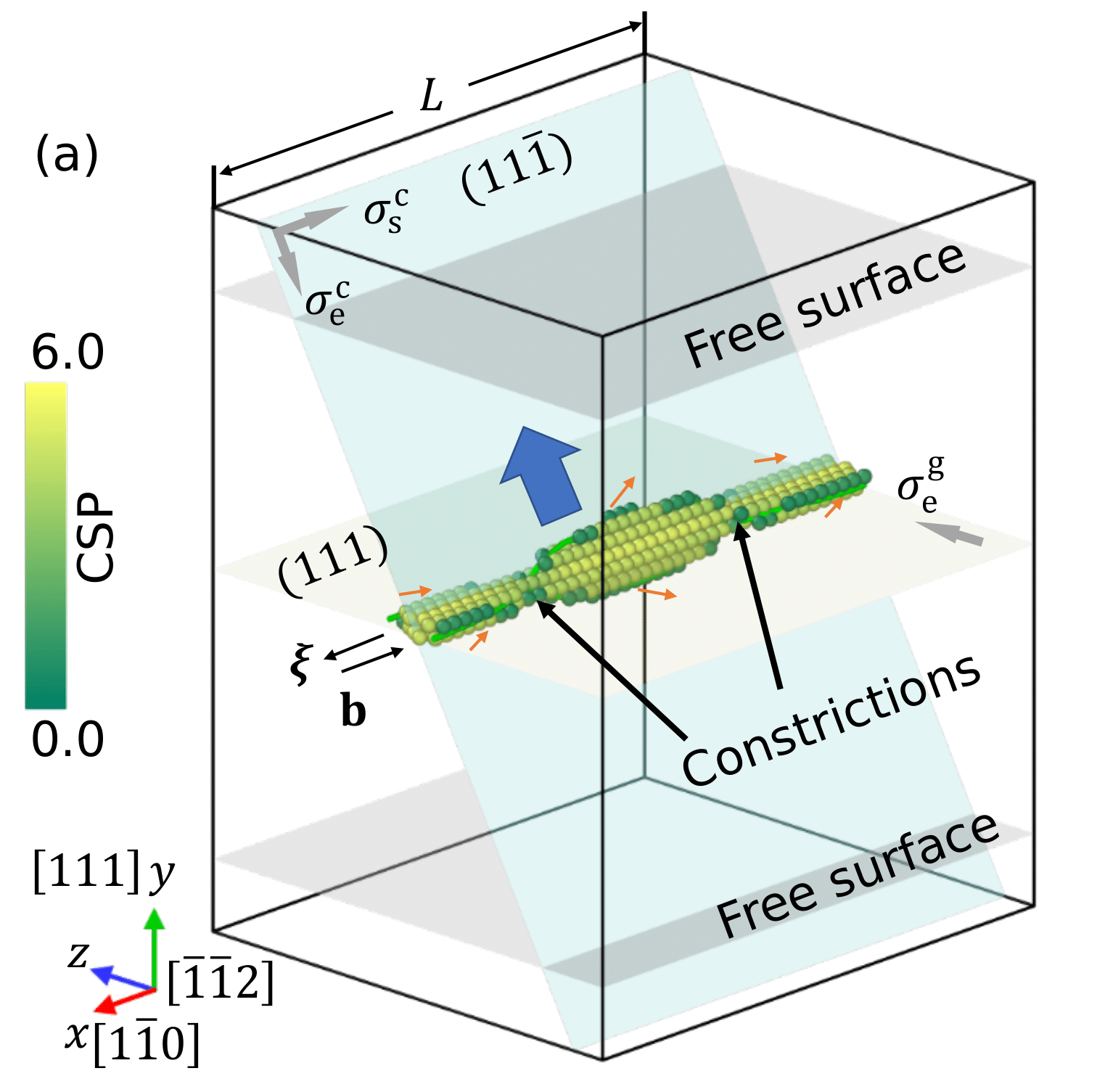
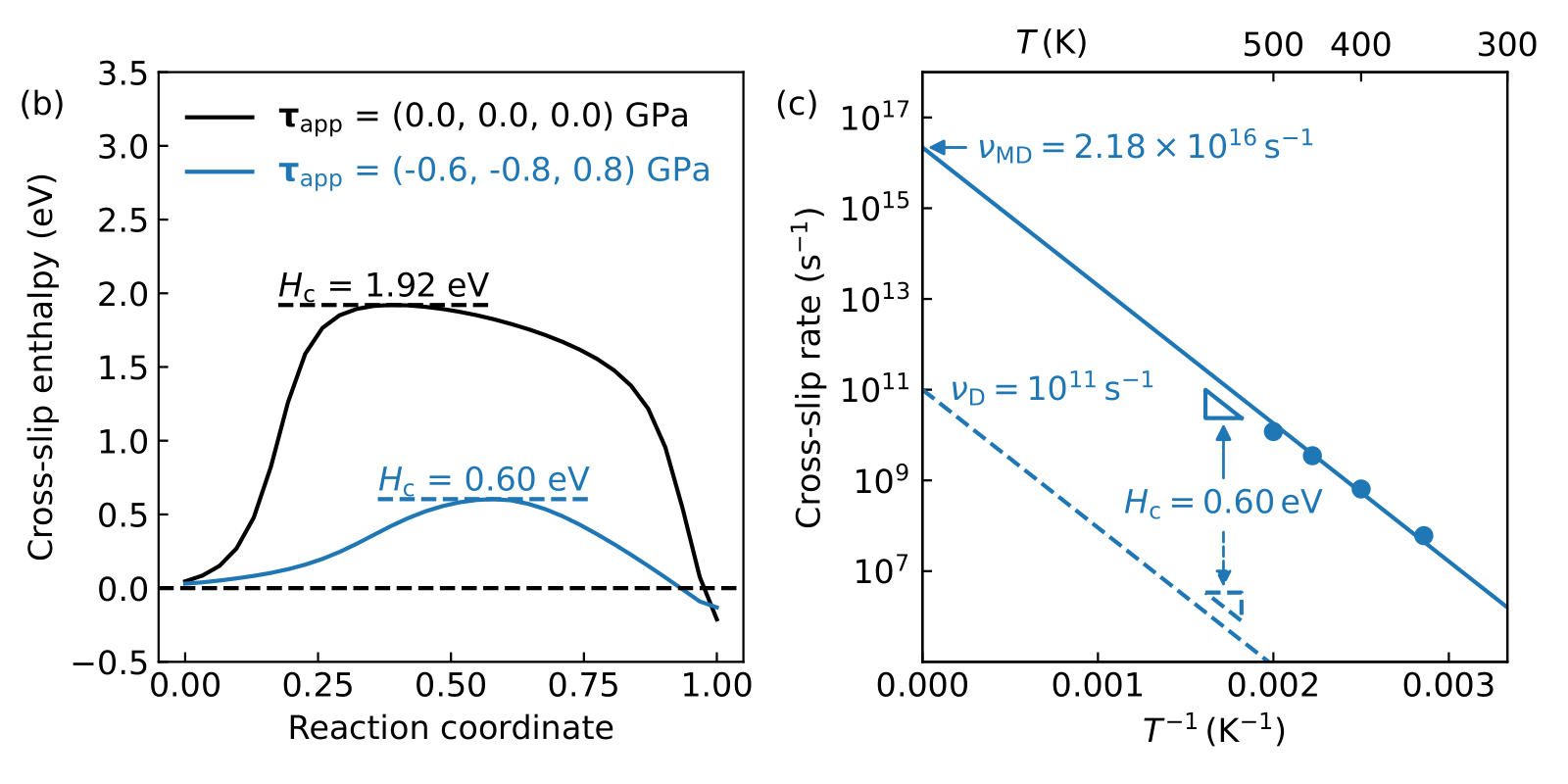
Dislocation cross-slip that controls the work hardening (a plasticity behavior beneficial to mechanical stability) in face-centered cubic metals. It has been found that transition-state theory (TST) underestimates the dislocation cross-slip rate under stress by three orders of magnitude when compared with direct molecular dynamics (MD) simulations. Based on thousands of energy barrier calculations exploring the entire stress space and thermodynamic analysis, I successfully explained this discrepancy by the activation entropy due to anharmonic effects such as thermal expansion and softening. Based on this understanding, an accurate rate model was developed to predict the cross-slip rate in a broad range of stress and temperature conditions. (2, 3)
The energy barrier for homogeneous cross-slip of a screw dislocation in face-centered cubic (FCC) nickel is calculated using atomistic simulations as a function of the Escaig stress on the glide plane, the Escaig stress on the cross-slip plane, and the Schmid stress on the cross-slip plane. Two cross-slip mechanisms, Friedel-Escaig (FE) and Fleischer, are examined and their energy barriers are calculated for a large number of stress combinations. For each mechanism, the energy barrier as a function of three stress components can be reduced into a one-dimensional function of an effective stress. The stress domains in which FE and Fleischer mechanisms operate respectively are determined. The FE mechanism dominates when the Escaig stress on the glide plane (in the direction that reduces the stacking fault width) is the largest stress component. Increasing the Schmid stress and Escaig stress (in the direction that expands the stacking fault width) on the cross slip plane promotes the Fleischer mechanism. The cross slip energy barrier functions obtained here can be used as input functions for computing cross slip rates in mesoscale dislocation dynamics simulations.
- Yifan Wang and Wei Cai, “Stress-dependent activation entropy in thermally activated cross-slip of dislocations,” Proceedings of the National Academy of Sciences, 120, 34, e222203912 (2023). (link).
- William P. Kuykendall, Yifan Wang, and Wei Cai. “Stress effects on the energy barrier and mechanisms of cross-slip in FCC nickel,” Journal of the Mechanics and Physics of Solids, 144, 104105 (2020). (link)
Reversible shear transformations governing anomalous temperature dependence of elastic limit in metallic glass

Shear-transformation zone (STZ) is considered the primary source of plastic deformation in metallic glasses. The formation of STZ is a thermally activated process whose energy barrier decreases with increasing strain. It is conventionally expected that the elastic limit (the onset of plastic deformation) occurs at earlier stress under higher temperatures since the higher thermal fluctuation can overcome higher energy barriers of the STZs. (4) However, I find that the elastic limit of metallic glasses can increase with increasing temperature because the STZs can convert from irreversible to reversible (5). This work pointed out that the reversibility of STZ is essential to macroscopic mechanical behaviors and provided a model that predicts the reversibility as a function of temperature. This work is also the first to investigate the strain dependence on the potential energy landscape, combining high-throughput molecular dynamics simulations and energy barrier calculations.
- W. L. Johnson and K. Samwer, “A universal criterion for plastic yielding of metallic glasses with a $(T/T_g)^{2/3}$ temperature dependence,” Physical Review Letters, 95 (19): 195501 (2005).
- Yifan Wang, Jing Liu, Jianzhong Jiang, and Wei Cai, “Reversible shear transformations governing anomalous temperature dependence of elastic limit in metallic glass,” to be submitted.
Spherical harmonics method for linear elasticity problems with spherical interfaces
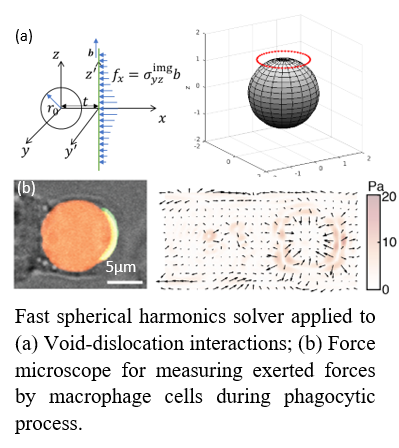
I developed a fast spherical harmonics solver that can solve 3D elasticity problems with arbitrary boundary conditions on a spherical interface. The solver pre-computed the elasticity solutions of all the spherical harmonic modes, thus simplify the solving process of the entire elasticity problem to spherical harmonic transformation and solving a sparse linear system. The solver outperforms general elasticity solvers such as the finite element method in both speed and accuracy (6). The solver package has been applied to void-dislocation interaction problems in solids. The package also enables particle-based force microscopes to measure forces exerted by macrophages during phagocytic processes (7, 8).
Related Papers:
- Yifan Wang, Xiaohan Zhang, and Wei Cai, “Spherical harmonics method for computing the image stress due to a spherical void,” Journal of the Mechanics and Physics of Solids, 126, 151 (2019). (link) (code)
- Daan Vorselen, Yifan Wang, Matt Footer, Wei Cai, and Julie Theriot, “Microparticle traction force microscopy reveals subcellular force exertion patterns in immune cell-target interactions,” Nature Communications, 11, 20 (2020). (link) (code)
- Daan Vorselen, Sarah R. Barger, Yifan Wang, Wei Cai, Julie A. Theriot, Nils C. Gauthier, and Mira Krendel. “Phagocytic ‘teeth’ and myosin-ii ‘jaw’ power target constriction during phagocytosis,” eLife 2021; 10:e68627 (2021). (bioRxiv) (code)
